The Associative Property of Addition and Multiplication is another fairly simple and straight forward property for developing number sense and understanding. The property simply states that in addition expressions and multiplication expressions, numbers can be grouped (or associate) differently without changing the value of the expression. What this means is:

In the first expression (2 + 3) + 4, the ‘2’ and ‘3’ are first added together to make ‘5’ according to the order of operations. The ‘5’ is then added to the ‘4’ to make the total of ‘9’ on the left side of the equation. In the expression on the right side 2 + (3 + 4), however, the ‘3’ and ‘4’ are added together first to make ‘7,’ which is then added to the ‘2’ at the beginning of the expression. The total on the right side of the equation is also ‘9.’

The property also applies to multiplication expressions. Consider the following:

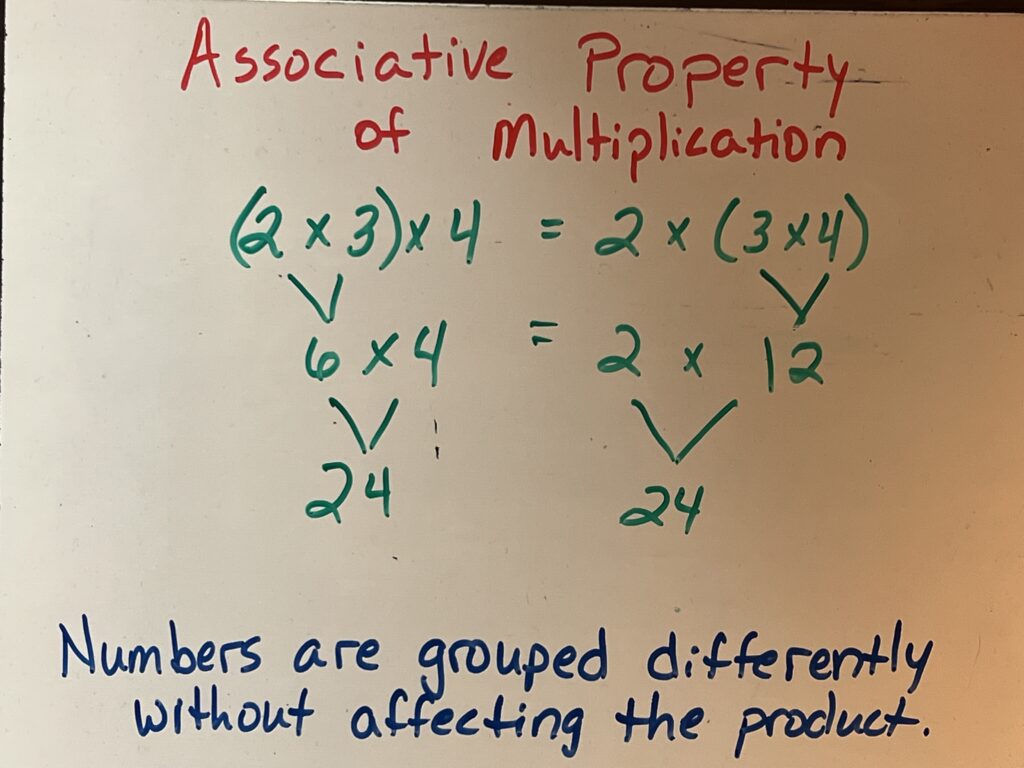
Both expressions have a product (multiplication answer) of 24. The order of the numbers in the expression make no difference.

One reason we use the Associative Property is to assist with number sense and mental math calculations. Regrouping the numbers in a string of addition or multiplication problems gives me the flexibility to look at the numbers in the expression in a different way to make numbers that are more compatible with one another for quick mental math calculations. Consider this example:

6 x 12 x 5

Working through this problem from left to right, I think that while I may know my facts for multiplying by 12, after multiplying ‘6 x 12′ to get ’72,’ I may NOT know how to take the ’72’ and multiply it by the remaining ‘5’ mentally. The Associative Property allows me to compute ’12 x 5′ first, which equals ’60’ (again, using my facts for multiplying by 12). I can then multiply ‘6 x 60’ mentally, to get ‘360.’ This is the same product I would have gotten if I had taken ’72 x 5′ earlier, but the problem may have seemed simpler in my mind because I used the Associative Property to group the numbers differently.

This is how the Associative Property applies to number sense and mental math.

This is what I am here to help you with. I am here to help you learn Mathanese, because I speak Mathanese, and you will, too. The focus of my blog is to present you with strategies to practice computational facts, explanations of number sense reasoning to understand computational processes, and teach you the Mathanese terms you need to succeed as a mathematician. Choose a topic that is listed in the menu to learn more. If a topic you want to learn about isn’t available, send me an email and ask me to write something about it.

If you haven’t done so already, subscribe to my email list so that you can be notified when I publish new posts. If you have questions about anything in this post, please reach out and ask for clarification. Thank you for reading and have a great day.

Mr. H.